钢结构稳定设计向来都是结构工程专业的难点,里边充斥着许多抽象、难理解、易混淆的概念,老版的国标钢结构设计规范未能做到清晰的、准确的传递给工程设计人员稳定相关规定,其中的一些过分简化、易误解的规定条款,让工程师在面对真实、复杂的项目时经常缺乏信心。
本文希望借助美标钢结构稳定的理论和方法的介绍,让读者建立起钢结构稳定的全局观,然后在这种全局认知的基础上,通过工程实践或规范学习,慢慢的填充细节。
我们将从一个基本概念开始,逐步增加钢结构稳定分析中的影响因素,直至达到目前规范要求的深度,并借此对比 DM ELM FOM 三种方法分别如何考虑这些影响因素。
美标中所有的构件的强度验算都可以以下公式来表达
Q < фRn
其中,Q 是 LRFD 的荷载效应,ф 是材料抗力系数,Rn 是构件的名义强度。以下的推演过程也将分荷载效应和抗力两部分描述。
STEP 0
起始的模型是基于以下假定:
荷载效应
1 结构没有任何初始缺陷
2 钢材为理想弹性体
3 不考虑二阶效应
即挺直杆件在 LRFD 组合下的一阶线弹性分析
抗力
1 构件强度能够达到截面屈服强度,即 P = fyA, M = fyZ
如果结构设计止步于此,那么设计院的工作将简单而美好。
STEP 1 二阶效应
二阶效应属于荷载效应的影响因素,不同于结构力学在未变形体建立平衡方程,二阶分析是在已变形体上建立平衡方程,下图是典型的二阶效应的示意图,二阶效应会放大结构在侧向力作用下的内力和位移。
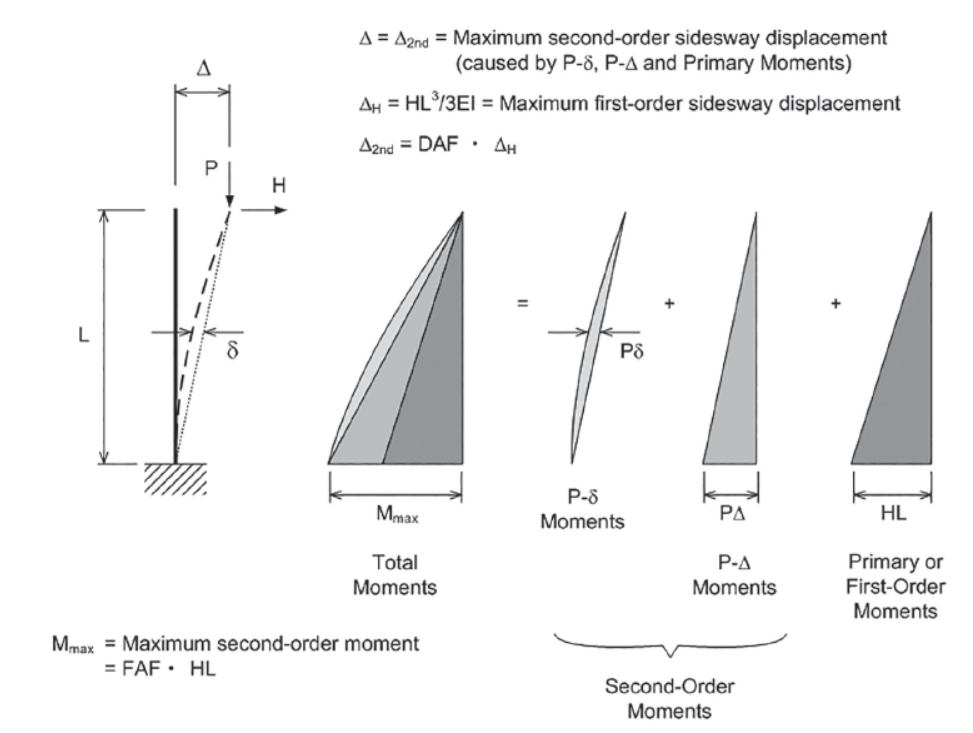
目前有两种方法考虑二阶效应,分别是
- 直接二阶分析法
目前主流的结构分析软件都支持二阶线弹性分析,注意二阶分析是同时考虑水平力和竖向力,所以不能使用传统的线性荷载组合,而应将带分项系数的水平力和竖向力同时放在一个工况中运行分析。
- 一阶分析放大法
即传统的考虑二小效应的近似方法,美标中对应的章节是 AISC 360-16 Appendix 8,通过系数 B1 B2 放大构件一阶分析的内力结果,同时系数 B2 也是楼层 P-Δ 效应的位移放大系数,是衡量 P-Δ 效应的重要指标,由楼层竖向力和楼层侧向刚度决定。

二阶效应放大了分析内力和位移,增加了荷载效应。
STEP 2 屈曲
屈曲是抗力的影响因素。细长的构件受压时易侧向失稳,这种现象叫做屈曲,这样的描述虽然不严谨,但联系我们生活经验,更容易理解。
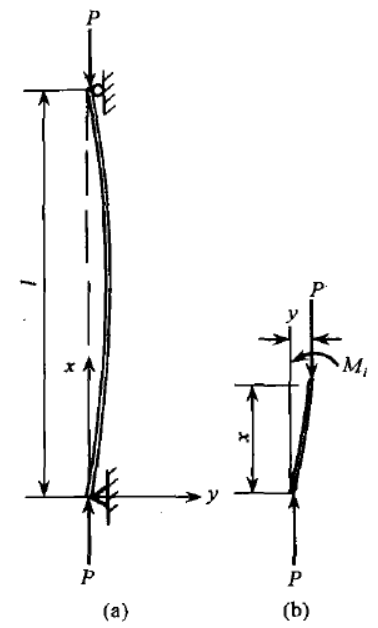
两端铰接轴心受压杆件的欧拉屈曲荷载为:
轴力 P = π2EI/l2
除以截面积 A,得到欧拉屈曲应力 Fe = π2E/(l/r)2
以长细比 l/r 为横坐标,截面应力 F 作为纵坐标,绘制构件的截面应力曲线
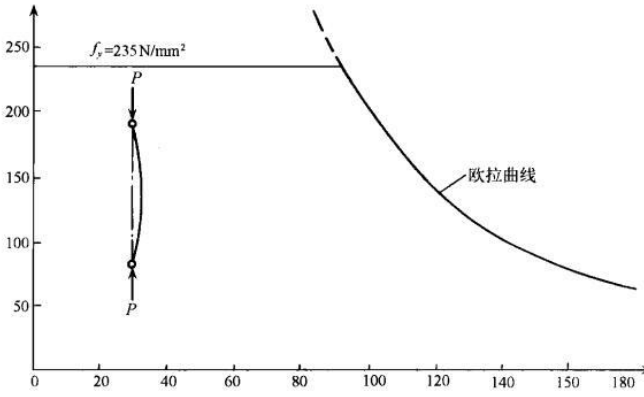
以 Fy 和欧拉曲线的交点为界限,长细比小于界限时屈服强度控制,长细比大于界限时欧拉屈曲控制。
梁的屈曲也是类似于上述情况,因为梁受弯时,一半的截面受压,这部分截面倾向于向弱轴屈曲,而受拉部分的截面阻止这种侧向屈曲的趋势,最终达成 lateral-torsional-buckling 的伴随着侧移和扭转的中间状态,如下图所示。
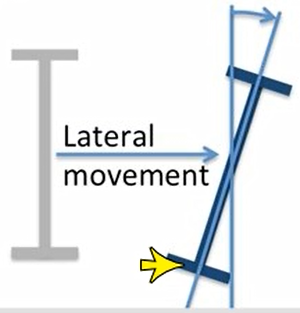
AISC 360-16 chapter E F 受压构件和受弯构件的计算公式中包含了屈曲的影响,使用时应注意假定条件,对于柱构件是两端铰接轴压假定,对于梁是两端铰接,扭转约束且沿构件长度均匀受弯的假定,当实际条件与默认假定不同时,还需要特殊考虑。
当构件足够细长时,屈曲效应降低了构件的强度,使其无法达到截面屈服强度。
有侧移 vs 无侧移
由两端铰接轴心受压推到的公式,可以演化出各种不同的边界条件。不同的边界条件带入微分方程后得到不同的解,将不同的解整理成欧拉屈曲公式的形式后,差异的部分归纳成系数 计算长度系数 k,此时欧拉屈曲应力公式变为 Fe = π2E/(kl/r)2。理想化的边界条件推导的计算长度系数见下表
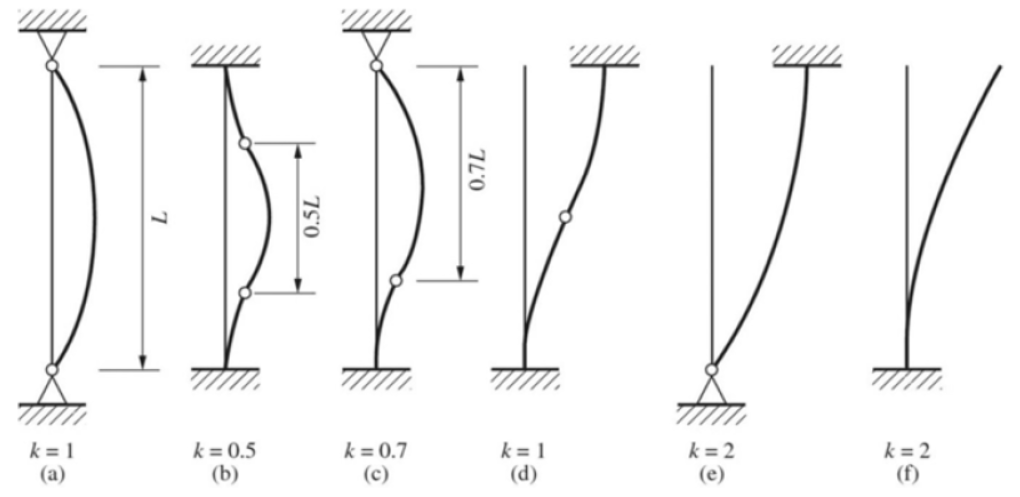
然而现实结构中不存在理想化的边界条件,没有完全的铰接和刚接支座,却都可以用具有一定刚度的弹簧支座来模拟,如下图所示
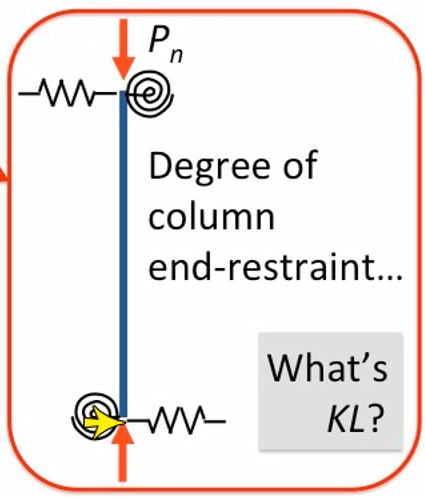
有两种方法可以求解计算长度系数 k
- 规范查表法
- 计算机屈曲分析
此时引入了有侧移和无侧移的概念,来描述框架失稳时的形态,因为这两种形态对应的计算长度系数 k 的计算方法不同。
这里要强调一点,规范查表法求得的 k 值,除了体现不同的边界条件以外,还赋予了其他的含义,是半经验半理论的数值;而计算机屈曲分析则单纯从边界条件的理论分析求解的。
STEP 3 初始缺陷
土木工程这个又土又木的专业,施工起来总存在误差,对粗壮的混凝土构件来说影响不大,但对于细长的钢结构构件的影响就不能忽略了,钢结构施工安装结束时存在两种缺陷,一种是沿构件长度的初始弯曲(out of straightness),另一种是结构垂直度的偏差(out of plumbness),这两种缺陷的存在使得柱受压时伴随着弯矩。
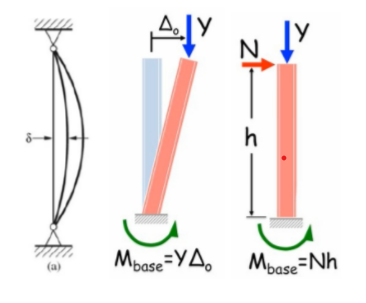
AISC 360 将构件缺陷(out of straightness)包含在轴压构件抗力计算公式中,而将体系缺陷(out of plumbness)等效成水平力 notional load,加载到重力作用点上,使得竖向力作用在有水平位移的结构上,增加了荷载效应。
构件缺陷降低了构件强度,而体系缺陷增加了荷载效应。
STEP 4 残余应力
残余应力是由热轧型钢在冷却过程中截面的不均匀收缩,或者在钢结构加工、焊接过程中残留在截面内部的初始应力,且内部自相平衡。

残余应力是造成结构非线性的主要因素,其他因素还包括弯矩的塑性发展和轴力对截面转动刚度的折减等,在 AISC 360 中都归类到结构非线性导致的刚度折减。结构非线性导致的刚度折减对构件抗力和荷载效应都能产生影响。
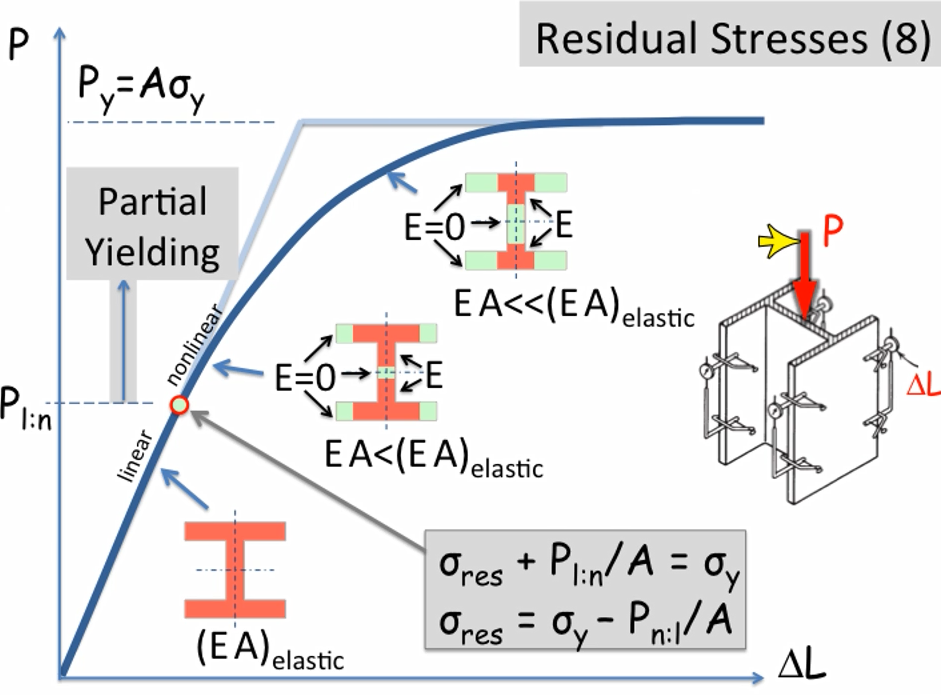
在构件抗力方面,因截面提前屈服达到弹塑性阶段,为了控制变形,规范将柱抗力曲线进一步降低,如下图所示。
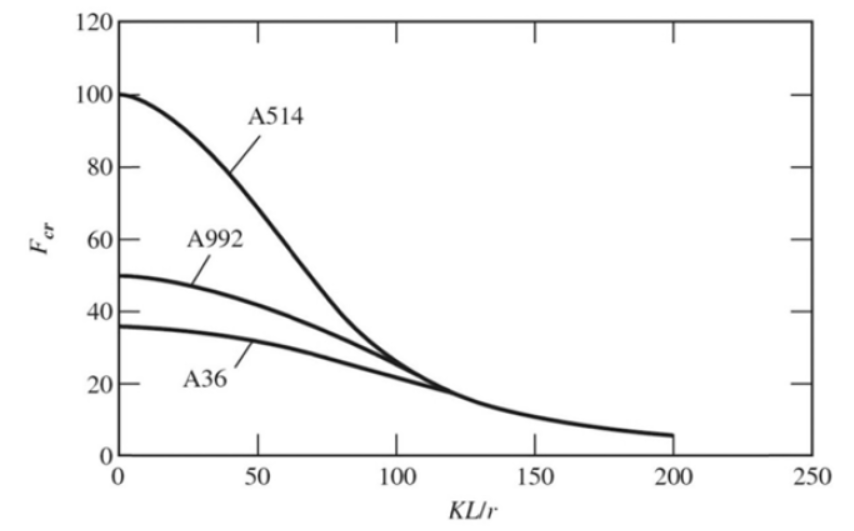
荷载效应方面,构件刚度的提前退化,直接影响了结构分析,导致变形增大,二阶效应增加,结构内力增大。
残余应力导致的刚度折减的存在降低了构件抗力,增大了结构变形。
DM ELM FOM 方法对比
DM: direct analysis method
ELM: effecitve length method
FOM: first order analysis method
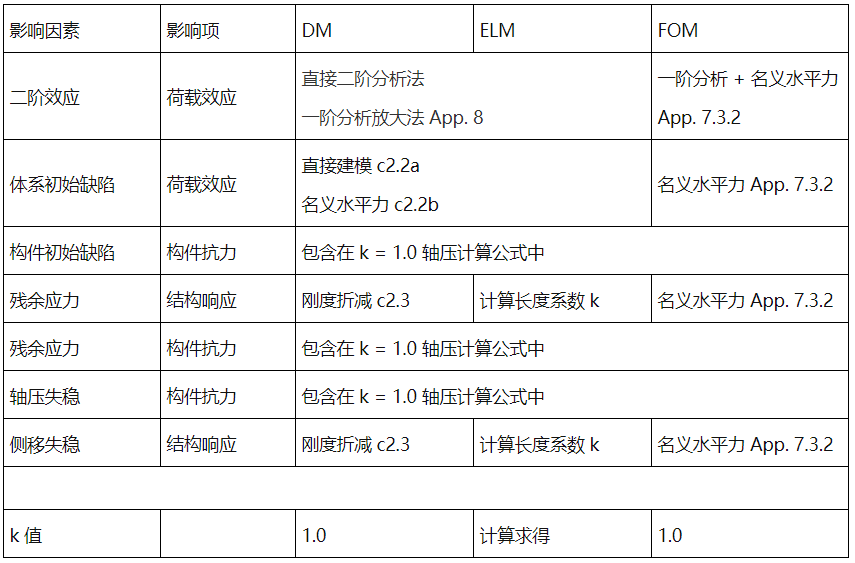
残余应力和侧移失稳对结构响应的影响,不同的方法采用了不同的途径,看似不相关的途径为何能实现同样的目的呢,其背后的理论原因是二阶分析和屈曲分析,本质上都是特征值分析,两者能推导出相同的临界荷载,而 DM 法规避了计算长度系数 k 值的计算,对于与规范查表法求 k 值的前提条件有出入的结构(即复杂,不规则结构)而言,DM 法大大简化了计算过程,并且能更真实的反应结构受力状态。
在 2016 版美标钢结构设计规范中,FOM 是基于 DM 法的一种简化方法,但需要满足 Appendix 7.3.1 的前提条件。DM 和 ELM 是主流的稳定分析方法。
本文通过概括性的介绍,定性描述的影响因素,试图呈现给读者钢结构稳定的大的轮廓,而其中的诸多细节,是无法在一篇文章中讲清楚的,主流的钢结构稳定的理论书籍大约有上千页的篇幅,很多高校中钢结构稳定是一个学期的课时,对于已工作人士,很难进行系统的学习,但当实际项目中遇到一些特殊问题时,确实需要扎实的理论背景知识,才能做出正确的决策,笔者的建议是有针对性的去理解概念,然后更多精力放在如何正确的应用稳定分析方法。
文末附上 Ronald D. Ziemian 教授讲座的视频链接,供大家参考学习。
